CONCEPT RECAPITULATION TEST - III [CONCEPT RECAPITULATION TEST - III]

other 12 Pages

Joint Entrance Examination (Main)

Concept Recapitulation Test

BSP

Contributed by

Bishnu Singh Pau

AITS-CRT-III-PCM(S)-JEE(Main)/14

FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
1

ANSWERS, HINTS & SOLUTIONS
CRT –III
(Main)

Q. No. PHYSICS CHEMISTRY MATHEMATICS
1.
A B A
2.
A D D
3.
C A B
4.
A A C
5.
C D A
6.
C A C
7.
A A D
8.
D B C
9.
B A B
10.
C A B
11.
A B C
12.
D C B
13.
D D A
14.
C B B
15.
C C C
16.
A D B
17.
B C B
18.
B C A
19.
B A C
20.
D B A
21.
A C C
22.
C D C
23.
C D D
24.
A D A
25.
C C B
26.
C C C
27.
A D C
28.
C D D
29.
A C B
30.
C B B

ALL INDIA TEST SERIES

FIITJEE

JEE (Main), 2014

From Classroom/Integrated School Programs
7 in Top 20, 23 in Top 100, 54 in Top 300, 106 in Top 500 All India Ranks & 2314 Students
from Classroom /Integrated School Programs & 3723 Students from All Programs have been Awarded a Rank in JEE (Advanced), 2013

Page 1
AITS-CRT-III-PCM(S)-JEE(Main)/14

FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
2

P
P
h
h
y
y
s
s
i
i
c
c
s
s PART – I

1. V = Es ;
E =
2
2sm
qt


2
2
2s m
V
qt
 = 11.375 Volt

.2
'
sin30 sin60

 
 


' 3

 

' 'cos30 vcos30
   


cos60 (v ' ') cos60 (2v) v
       
 

 = v/ =
40 3
400
0.1 3
 rad/s



30


120°









v

3. for x<0
It will oscillate like SHM
Time period
1
m
T
k
 
For x>0
It will perform periodic motion under constant force

2
2
2E
T 2
mg

Hence time period
1 2
T T T
 

2
m 2E
T 2
k
mg
  

4
2
0
0
mv
ev B
R


0
mv
B
eR


2 2
a R b R
  

2 2
b a
R
2b



0
2 2
2bmv
B
(b a )e



Page 2
AITS-CRT-III-PCM(S)-JEE(Main)/14

FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
3

5. Here the total time is given T
Time spent m the region is
( 2 )
  

Hence total time spent

2
T
2
  
 

 

 




2
  
v

2
  
v

6. Torque of Internal force is always zero. All other quantities will vary.

8. Static friction depends on tendency.

9.
2 2
2
ML 3ML
sin 60 2
12 24
 

10. When impulse of external force is zero.

11. Balance forces.


N



R

mg

m

2
L cos


N



(





)

12.

I

I

13. y(x, t) =
2
a
x
t
b
e
 
 
 
 
 
 
 
 v = b

15. 2L = m  (
1
/2) =
m T
2f 9


L = n  (
2
/2) =
n T
2f 4


 m = 3n = 3  1 = 3

16. cos  = 1   = 0  L = 1/C

17. f
B
= f  f
0
=
0
0 0
0
v v sin30
f f
v v sin30
 
 

 
 
 

=
0 0
0
2v f
2v v


Page 3
AITS-CRT-III-PCM(S)-JEE(Main)/14

FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
4

18.
2
1
mv h
2
 

19.  = D/d,  is minimum for violet.

20.
PG PC CG
ˆ ˆ
V V V 2xj 2i
   
  

Hence, for the paritcle,
V
x
= 2m/s and V
y
= 2x = 4t
a
x
= 0 a
y
= 4m/s
2

x = 2t, y = 2t
2

 a
Total
= 4m/s
2

(a) (along Y-axis)
and trajectory 
2 2
x x
y 2.
4 2
 

when
N
a a
 

 , a cos  = a sin    = 45º
So, V
x
= V
y
= 2  V =
2 2


2
C
o
N
V 4 2
R 2 2
a 4.cos45

   m =
4
m
2

Page 4
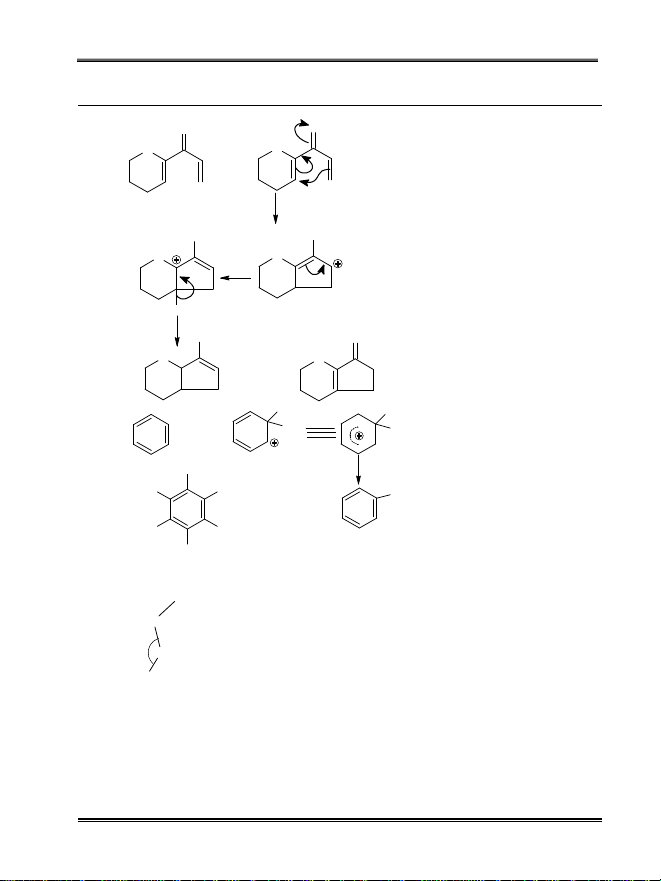AITS-CRT-III-PCM(S)-JEE(Main)/14

FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
5

C
C
h
h
e
e
m
m
i
i
s
s
t
t
r
r
y
y PART – II

2.
O
O
H


O
OH
O
OH
O
OH
H
O
OH
Tautomerise


O
OH

3.
D

 
H
D
H
D
H


D
3
D O

  
D
D
D
D
D
D

4. Talc has empirical formula Mg
2
(Si
2
O
5
)
2
Mg(OH)
2
which
 
2n
2 5
n
Si O

units of two dimensional sheet
silicates.
5.
O
H
O
H
97
o
It has half open book like structure having dihedral angle 97
o

6.








o o 1
r r 2 4
H 2 46.1 187.8 2 285.8 H N H kJ / mol

       
= - 241.0 kJ/mol
-1



o
2 4
r
H N H 50.6 kJ / mol
 
Decomposition enthalpy = - 50.6 kJ/mol.
9. Radius ratio for MgO is = 0.464 which reflect the coordination number 6 and radius ratio for MgS
is 0.353. Which reflect the coordination number 4.
Page 5
AITS-CRT-III-PCM(S)-JEE(Main)/14

FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
6

10.








2 3 4
H O ClO aq ClO aq 2H aq 2e
   
   










3 2 2
2H aq ClO aq 2e ClO aq H O
   
   








3 2 4
2ClO aq ClO aq ClO aq
  
 

o
cell
E 0.33 0.36 0.03
   

o
cell
RT
E lnK
nF
 (at equilibrium)

0.059
0.03 logK
2
 
logK = - 1
K = 0.1

3 4 2
2ClO ClO ClO
Initially .1 0 0
equilibrium .1 2x x x
  





 
2
2
x
K
.1 2x



 
2
2
1 x
x 0.019 M
10
.1 2x
  


12. Probability of finding an electron is zero, i.e.
2
0
 
.

 
 
2
3/2
2 /2
0
1 1
1 8 12 e 0
a
16 4

 
 
 
 
      
 
 
 
 
 





2
1 8 12 0
      

On solving for  we get
 = 1, 6, 2 and
0
2r
a
 
For  = 1;
0
0
a
2r
1 r
a 2
 

0
0
2r
2; 2 r a
a
   

0
0
2r
6; 6 r 3a
a
   
13. n-factor of H
3
PO
2
is 4/3 for the reaction.
14.
b b
T K m i
   

2.08 = 0.52 × 1 × i
i = 4
This implies that the salt on dissociation gives 4 ions. Thus, the salt that gives four ions is
K
3
[Fe(CN)
6
].
Page 6
AITS-CRT-III-PCM(S)-JEE(Main)/14

FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
7

15.
D
H
O
CH
3
H


D
H
O
+
CH
3
H

OH
H
CH
3
D
-D shift
OH
D
CH
3
H
H



OH
D
CH
3

16. O
2
SeO

O
O
OH
Bezilic acid rearrangement

OH
COO
 
B
 
C

18. It is a non-degradable pollutant.
19. Colloidal silver bromide solution is used in photography.
20. Stability of carbonates increases down the group. Carbonates of alkali metals are more stable
than those of alkali metals.
21.
2px

and
2py

have one nodal plane each. In 1s there is no nodal plane and in case of
*
2px

there
are two nodal planes.
22. Le-Chatellier’s principle.
25.
COOH
2
SOCl

COCl
3
AlCl / 
O
Zn/Hg
HCl


26.
4
NH Cl Nesseler's reagent Brown colour of iodide
million's base.
 

Page 7
AITS-CRT-III-PCM(S)-JEE(Main)/14

FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
8

M
M
a
a
t
t
h
h
e
e
m
m
a
a
t
t
i
i
c
c
s
s PART – III

1. Using T = S
1
take mid–point (h, k) then equation of PQ is
xh + yk – (h
2
+ k
2
) = 0 ….. (1)
mx – y + 2m = 0 ….. (2)
Compare (1) and (2) eliminate m

2. As f(x) is continuous decreasing function on (0, ), so 0 < f(8x) < f(6x) < f(4x)
So


 


 
x x x
f 6x f 4x
lim 1 lim lim
f 8x f 8x
  
 
By squeeze play theorem


 
x
f 6x
lim 1
f 8x



3. The given lines will be parallel to lines ax
2
– 6xy + y
2
= 0
So,
2
y y
6 a 0
x x
   
  
   
   

m + m
2
= 6 ….. (1)
Which gives m = –3 or 2
and mm
2
= a ….. (2)
From (2) a = –27 or 8
Hence sum of all possible value of a = –19

4.
 
 
2
x
4
lim
x
2
e lng 2 x lng 2

 
 
 

0
form
0
 
 
 



 
 
 
 
x 0
2
g' 2
lim
1
2
g 2
2
g' 2 x
2x
1
g 2 x
e e e
2x
e




 

  

5.
 
1/ n
0
n
2
f t dt
I lim
1
n




0
form
0
 
 
 

Using : L’ Hospital and using Leibnitz rule

3
2
n n
1 1
n f
n 1
n
n
I lim lim f
2 2 n
 
  

 
 
 
 
 
 
 
  

Put
1
n
h

hence





 
h 0
1 f 0 h f 0 1
I lim f ' 0
2 h 2

  
  
 
 

6. For xy = 1 
2
dy 1
dx
x
 
Slope of normal to xy = 1 for x
2
> 0 (x  0)
Slope of line (given) =


2
2
log 1 5a a
0
5
 


So 1 + 5a – a
2
> 1
Page 8
AITS-CRT-III-PCM(S)-JEE(Main)/14

FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
9

a
2
– 5a < 0 hence a  (0, 5)

7.
2
a
3


1 1 2 2 2
ah
2 2 3
3 3
     

  
 
 
abc 2 1 1 3 3
R
4
3 4 2 2 2
  


A

1

1

M

a

B

C

2
3

1
3

1
3

8. Area of the parallelogram outside the circle
= Area of parallelogram – Area of sector OPQ
=
 
1 1
sin 2 sin f
2 2 2

 
       
 
 

Q

R

P

O



r = 1

9. Using


 
n n 1 n 2
r r 1 r 2
n n n 1
C C C
r r r 1
 
 

   

is equal to

10. We have |(A
–1
) adj(B
–1
) adj(2A
–1
)| =
2 2
1 1 64
A
B A
  =
64
8
2 1 4
 
  

(By using |A
–1
| =
1
A
and |adj B| = |B|
n–1
where n is order of square matrix)

11. This distance between the given parallel lines (h) is
1
5

length of the side of triangle is =
2h
3

Area of triangle =
2 2
3 4h h 1
4 3
3 5 3
  

12. The volume of tetrahedron =
1 0 0
1 1 1
OA OB OC 1 1 0
6 6 6
0 1 1
 
 
 
  

Area of base =
   
1 1
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ
i j i j k i i k
2 2
      
=
 
1 1
2
2
2

Hence height =
3 volume 3 2 1
Area of base 6
2

 

13. C = 20

1
ab
2
 
S – a = 7
S – b = 13
a – b = 6 ….. (1)
a
2
+ b
2
= 400

C

b

A

7

D

13

B

a

Page 9
AITS-CRT-III-PCM(S)-JEE(Main)/14

FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
10

(a – b)
2
+ 2ab = 400
 ab = 182

1
ab 91
2
  

14. Let
ˆ ˆ ˆ
r xi yj zk
  


Comparing x = t
2
+ t – 2  y = t + 2  z = t
2
+ 6t + 9
Hence z – x = 5t + 11  z – x = 5(y – 2) + 11  x + 5y – z + 1 = 0

16.
a b a b 8
 
 
 
 
 


2
a b 8
 



2
2
2
a b sin 8
 



2
2
8
b 16
1
1
2
 


b 4



17. If
2 2
2 2
x y
1
a b
 
, a > b
So x
1
x
2
= y
1
y
2
= b
2

3d = 49

3d 7


(x
1
y
1
)

(x
2
y
2
)

y
1

y
2

18. f(x) = sec x – cosec x
f(x) = 0 at x
4



Also
f " 0
4

 

 
 
so f(x) is minimum at x
4



/ 4 / 2
0 / 4
f sec d cosec d
4
 


 
     
 
 
 
=
2 1
ln
2 1
 

 

 
=


2ln 2 1


19.
 
 
a a
0 0
cos a x
ln cota tanx dx ln dx
sina cosx
 

 
 

 
 

=
 
a a a
0 0 0
lncos a x dx lnsinadx lncosxdx
  
  

I(a) = – ln (sin a) · a
I(1) = – ln (sin a) = ln |cosec 1|

20. Let
1/ x
x 1
x 0
1
A lim 2
2


 
 
 
 
(1


form)
=
x
x 1
x 0 x 0
1 1 2 1
lim 2 1 lim
x 2 2x
e e

 
 

 
 
 
 
   
 =
1
ln2
2
e 2


Page 10

CONCEPT RECAPITULATION TEST - III [CONCEPT RECAPITULATION TEST - III]

CONCEPT RECAPITULATION TEST - III [CONCEPT RECAPITULATION TEST - III]

Download this file to view remaining 2 pages